关系的性质

重点：(1) 掌握自反性，反自反性，对称性，反对称性，传递性的定义及关系矩阵和关系图的特征，

　　　(2) 掌握关系五种性质的判断和验证。

一、关系的五种性质(自反，反自反，对称，反对称，传递)。

　　定义及关系矩阵，关系图特征由下表给出( 为上关系)

　　例1、，上关系：

　　判断以上关系各有哪些性质。

　　解：(1) 既不是自反又不是反自反，是对称的，不是传递的。

　　　　(2) 是反自反的，反对称的，传递的。

　　　　(3) 既不是自反又不是反自反的，既是对称又是反对称的，传递的。

　　　　(4) 是自反的，既不是对称又不是反对称的，不是传递的。

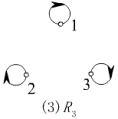
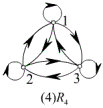
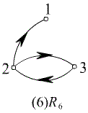
　　例2、判断下图中的关系分别具有哪些性质。

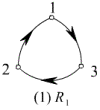
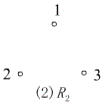
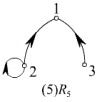
　　解：(1) 是反自反，反对称，不是传递的。

　　　　(2) 是空关系，是反自反，既是对称又是反对称的，传递的。

　　　　(3) 是恒等关系，是自反的，既是对称又是反对称的，传递的。

　　　　(4) 是全域关系，是自反的，对称的，传递的。

　　　　(5) 既不是自反也不是反自反的，反对称的，传递的。

　　　　(6) 是反自反的，既不是对称又不是反对称，不是传递的。

　　自反与反自反不交，存在既不是自反又不是反自反的关系。

　　对称与反对称相交，存在既是对称又是反对称的关系，也存在既不是对称也不是反对称的关系。

二、五种性质的其它判断方法

　　设是上关系，为上恒等关系，则

1、是自反的当且仅当，

2、是反自反的当且仅当，

3、是对称的当且仅当，

4、是反对称的当且仅当，

5、是传递的当且仅当。

　　要判断一个关系是否具有某些性质，除了可用定义判断外，以上五条也可用于判断。一般，五种性质中，传递性较难判断，注意到与传递性的定义，“若且，则 ”的共同点及不同点，有助于理解以上第五条的含义。

　　例3、设，上关系，，判断是否传递的。

　　解：因，所以是传递的。

　　因，所以不是传递的。

三、关系在各种运算下保持原有特性问题

　　设为上关系，它们具有某些性质，在经过并，交，相对差，求逆，合成等运算后，能否保持原有的特性，结论在下表中给出，“√”表示肯定，“×”表示否定。

　　以上表格中，肯定的可以证明，否定的可以举出反例。

　　例如：设为上的对称关系，证明也是上的对称关系。

　　证明：对任意

　　所以在上是对称的。

　　又如：设为上反对称关系，证明不一定是上的反对称关系。

　　反例：都是上的反对称关系，但不是上的反对称关系。