关系的运算
重点：(1) 掌握逆关系，合成关系的概念及求法，
(2) 掌握关系
次幂的概念及性质。
因为关系是有序对的集合，所以有关集合的运算，如交，并，差，补等对关系都适用，除此外，关系的逆运算，合成运算(也称复合运算)是两种重要的运算。
1、关系的逆。
(1)定义：关系 
的逆关系定义为 
。
例1、 
， 
为 
上小于等于关系， 
为
上整除关系，分别求出 
， 
。
解：
即
为
上大于等于关系。
即
为
上的倍数关系。
(2) 
的关系矩阵 
与
的关系矩阵 
，满足 
的转置。
如例1中
， 
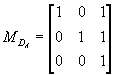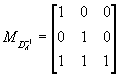
即 
与 
互为转置矩阵。
的关系图只需将
的关系图中的有向弧改向即得。
如例1中，
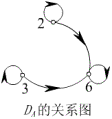
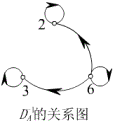
(3) 
。
2、关系的合成 (复合)
(1)定义，关系
和 
的合成关系定义为：
在定义中， 
起着中介作用，它与
和
都有联系，但
不在 
中直接出现。
例2、设 
，求
， 
， 
， 
， 
， 
。
解：
，
，
，
，
，
。
(2)
的关系矩阵 
与 
的关系矩阵 
满足 
。
注意：右式中的两个布尔矩阵( 
矩阵)相乘时，用到的加法应是逻辑加法，即：
， 
， 
， 
。
的关系图可将
的关系图连接起来求得。
如例2中，
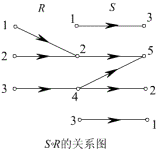
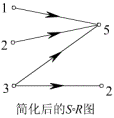
(3)
合成关系满足结合律： 
。
(4)
关系
的
次幂。
定义：设
为
上关系， 
，
的 
次幂规定为：
① 
② 
次幂的运算满足： 
， 
例3、 
，求 
， 
。
[解法一]用集合表示。
[解法二]用关系图表示。
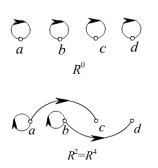
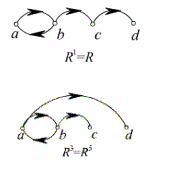
[解法三]用矩阵表示(略)。
3、关系的逆与合成间的联系。
证明：任取 
故 。
，
，
。
显然， 
为 中所有有序对的第一个元素构成的集合，
为
中所有有序对的第二个元素构成的集合。
例4、分别求出以下关系的定义域和值域。
(1) 
(2) 
(3) 
(4) 
解：(1) 
(2) 
(3) 
即偶数集
(4) 
