格与布尔代数
重点：格与布尔代数的有关概念及例子。
定义：设 
是偏序集，如果对 
， 
都有最小上界 (记 
)和最大下界 (记 
)，则称 
关于 
构成一个格。
其中符号 
可看成 
的二元运算，并非命题逻辑中的联结词符号。格
也记作 
。
例1、设 
为正整数， 
表示 的所有正因子的集合， 
表示整除关系，则 
构成格， 
，
的最小公倍数
的最大公约数
如： 
，
，
，
。
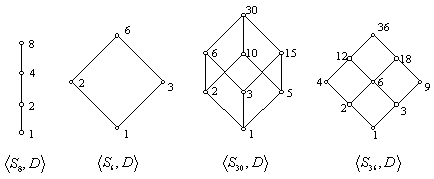
下图给出了格 
， 
， 
， 
例2、判断下图中的偏序集是否构成格，并说明理由。
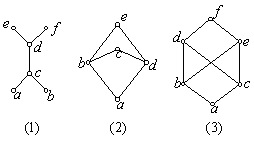
解：都不是格。
(1) 
没有上界。
(2) 
有上界 
，但无最小上界。
(3) 
有上界 
，但无最小上界。
1、对偶原理：设 
是含有格中的元素以及符号 
的命题，令 
是将 中的 
分别改写成 
所得到的命题，称为 的对偶命题。若 对一切格为真，则 也对一切格为真。
2、性质：设 为格，则运算 
和 
适合交换律，结合律，幂等律和吸收律，即 
，有
(1)交换律 
， 
(2)结合律 
， 
(3)幂等律 
， 
(4)吸收律 
， 
以上每组定律都是互为对偶的两个命题。
三、分配格，有界格，有补格。
分配律指： ， 
。
全上界指存在 
，对 
，有 
。
全下界指存在 ，对 ，有 
。
全上界记为 
，全下界记为 
，有界格也记为 
。
3、有补格——有界格 ，若对 
，存在 
的补元 (记 
)，使 
， 
，则称为有补格。
4、有补分配格——有补格且是分配格。
例3、所有的有限格 (指格中的元素有限个)都是有界格。
如例1中，格 中的全上界为 ，全下界为 。
但 和 不是有补格 (思考：为什么？)
是有补格， 
互为补元， 
互为补元。
是有补格， 
互为补元， 
与 
， 
与 
， 
与 
互为补元。
例4、判断下图中所表示的格是否有补格。
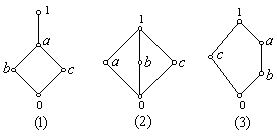
解：(1) 不是有补格，因只有 
互为补元， 
均无补元。
(2) 是有补格， 互为补元， 中任两个互为补元。
(3) 是有补格， 互为补元， 
的补元是 
， 的补元是 和 
。
5、有补分配格中任意元素的补元是唯一的。
1、定义：有补分配格称布尔代数，记为 
，其中“ 
”表示求补运算。
例5、(1) 集合代数 
是布尔代数。
(2) 开关代数 
是布尔代数，其中 为与运算， 为或运算， 
为非运算。
2、性质。
设 为布尔代数，则
(1) ， 
，
(2) 
， 
德·摩根律
3、有限布尔代数的表示定理
对每个有限布尔代数 ，都存在一个有限集合 ，使得 与其同构。
由这个定理知，有限布尔代数的元素只能是 
个，即 
。