重点：1、有向图，无向图的定义，
2、图中顶点，边，关联与相邻，顶点度数等基本概念，
3、各顶点度数与边数的关系 
及推论，
4、简单图，完全图，子图，补图的概念，
5、图的同构的定义。
图的基本概念
1、定义。
无序积 
。
在无序积中， 
。
无向图 
，其中 
为顶点(结点)集， 
为边集， 
，
中元素为无向边，简称边。
有向图 
，其中
为顶点(结点)集，
为边集， 
，
中元素为有向边，简称边。
有时， 
泛指有向图或无向图。
2、图的表示法。
有向图，无向图的顶点都用小圆圈表示。
无向边 
——连接顶点 
的线段。
有向边 
——以 
为始点，以 
为终点的有向线段。
例1、(1) 无向图
， 
，
(2) 有向图
，
，
图形表示如下：
注：常用字母 
表示边，如(1)中用 
表示 
， 
表示 
，…，(2)中也可用
表示有向边 
，…。
3、相关概念。
(1)有限图—— 
都是有限集的图。
阶图—— 
的图。
零图—— 
的图。特别，若又有 
，称平凡图。
(2)关联 (边与点关系)——设边 
(或 
)，则称 
与 
(或 
)关联。
无环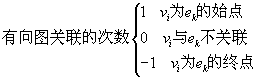 
孤立点——无边关联的点。
环——一条边关联的两个顶点重合，称此边为环 (即两顶点重合的边)。
悬挂点——只有一条边与其关联的点，所对应的边叫悬挂边。
(3)平行边——关联于同一对顶点的若干条边称为平行边。平行边的条数称为重数。
多重图——含有平行边的图。
简单图——不含平行边和环的图。
如例1的(1)中，
与 
关联的次数均为 
，
与 
关联的次数为 
，边 
都是相邻的， 
为孤立点， 
为悬挂点， 
为悬挂边，
为环， 
为平行边，重数
，
为多重图。
4、完全图
设
为 
阶无向简单图，若
中每个顶点都与其余 
个顶点相邻，则称
为
阶无向完全图，记作 
。
若有向图 
的任一对顶点 
，既有有向边 
，又有有向边 
，则称
为有向完全图。
例如：
1、顶点的度数 (简称度)。
无向图
，
的度数记 
，指与
相关联的边的条数。
有向图
，
的度数 
，其中 
称出度，指以
为始点的边的条数， 
称入度，指以
为终点的边的条数。
最大度 
最小度 
对有向图相应地还有最大出，入度，最小出，入度，分别记为 
， 
， 
， 
。
如例1的(2)中， 
， 
设 
为图
的顶点集，称 
为
的度数序列。
2、握手定理。
定理1：设图
为无向图或有向图，
， 
( 
为边数)，则
。
推论：任何图中，度为奇数的顶点个数为偶数。
定理2：设
为有向图，
，
，则
。
例2、(1) 
， 
能成为图的度数序列吗？为什么？
(2) 已知图
中有 
条边， 
个 
度顶点，其余顶点的度数均小于
，问
中至少有多少个顶点？为什么？
解：(1) 由于两个序列中，奇数的个数均为奇数，由握手定理的推论知，不能构成图的度数序列。
(2) 因 
，由握手定理知，
中各顶点度数之和为 
，
个
度顶点占去 
度，还剩 
度，其余顶点的度可能为 
，若全为
度顶点，则还需
个顶点，所以
至少有
个顶点。
1、子图定义：设
， 
是两个图，若 
，且 
，则称 
是
的子图，
是
的母图，记作 
。
真子图——
且 
(即 
或 
)。
生成子图——
且 
。
导出子图——非空
，以 
为顶点集，以两端均在
中的边的全体为边集的
的子图，称
的导出子图。
——非空
，以 
为边集，以
中边关联的顶点的全体为顶点集的
的子图，称
的导出子图。
例3、
上图中，(1)－(6)都是(1)的子图，其中(2)－(6)为真子图，(1)－(5)为生成子图。
2、补图定义。
设
为无向完全图， 
， 
为无向简单图，其中 
， 
，则称 
， 
相对于
互为补图，记 
， 
。
如例3中，(1)为完全图 
，(2)，(3)互为补图，(4)，(5)互为补图。
定义：设两个无向图 
， 
，若存在双射函数 
，使得对于任意的 
，当且仅当 
，并且 
与 
重数相同，则称
与
同构，记作 
。
例4、判断以下哪些图是同构。
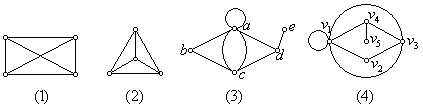
上图中， 
， 
， 
，
其中
，顶点间 
， 
， 
， 
， 
。
，顶点间
，
，
，
，
， 
。
但是(5)，(6)不同构，因在(6)中存在
个彼此不相邻的顶点，而在(5)中找不到。
例5、(1) 画出
个顶点，
条边的所有非同构的无向简单图。
解：只有如下
个图：
(2) 画出
个顶点，
条边的所有非同构的有向简单图。
解：只有如下
个图：
