图的矩阵表示
重点:1、有向图,无向图的关联矩阵,
2、有向图的邻接矩阵。
1、设无向图 ![]() ,
, ![]() ,
, ![]()
![]() 的关联矩阵
的关联矩阵 ![]()

例1、无向图 ![]() (下图所示),求
(下图所示),求 ![]() 。
。

解: 
2、性质。
(1) ![]() ,列和为
,列和为 ![]() ,表示每条边关联两个顶点
(环关联的顶点重合)。
,表示每条边关联两个顶点
(环关联的顶点重合)。
(2) ![]() ,第
,第 ![]() 行元素之和为
行元素之和为 ![]() 的度数。
的度数。
(3) ![]() 握手定理
握手定理
(4) ![]() ,当且仅当
,当且仅当 ![]() 为孤立点。
为孤立点。
(5) 若第 ![]() 列与第
列与第 ![]() 列相同,则说明
列相同,则说明 ![]() 与
与 ![]() 为平行边。
为平行边。
1、设无环有向图 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的关联矩阵
的关联矩阵 ![]() ,
,
其中 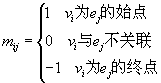
例2、有向图 ![]() (下图所示),求
(下图所示),求 ![]() 。
。
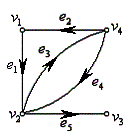
解: 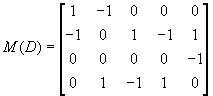
2、性质。
(1) ![]() ,列和为
,列和为 ![]() ,表示每条边有一起点,一终点。
,表示每条边有一起点,一终点。
(2) ![]() ,第
,第 ![]() 行元素的绝对值之和,即
行元素的绝对值之和,即 ![]() 的度数为
的度数为 ![]() 。
。
(3) ![]() ,所有元素之和为
,所有元素之和为 ![]() ,“
,“ ![]() ”个数
”个数 ![]() “
“ ![]() ”个数
”个数 ![]() 。
。
1、设有向图 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的邻接矩阵
的邻接矩阵 ![]() 。
。
其中 ![]() 指
指 ![]() 邻接到
邻接到 ![]() 的边的条数 (非负整数)。
的边的条数 (非负整数)。
例3、有向图 ![]() (下图所示),求
(下图所示),求 ![]() 。
。
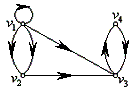
解:  。
。
2、性质。
(1) ![]() ,第
,第 ![]() 行元素之和,即
行元素之和,即 ![]() 的出度。
的出度。
(2) ![]() ,第
,第 ![]() 列元素之和,即
列元素之和,即 ![]() 的入度。
的入度。
(3) ![]() ,所有元素之和为
,所有元素之和为 ![]() 中边的总数,也可看成
中边的总数,也可看成 ![]() 中长度为
中长度为 ![]() 的通路总数。
的通路总数。
(4) ![]() 为
为 ![]() 中环的个数,也可看成
中环的个数,也可看成 ![]() 中长度为
中长度为 ![]() 的回路总数。
的回路总数。
3、求 ![]() 中长度为
中长度为 ![]() 的通路数和回路数。
的通路数和回路数。
(1) 令 ![]() 矩阵乘法
矩阵乘法
![]()
其中 ![]()

![]() 表示从
表示从 ![]() 到
到 ![]() 长度为
长度为 ![]() 的通路数
的通路数 ![]() 或回路数
或回路数 ![]() 。
。
考虑 ![]() ,简记为
,简记为 ![]() 。
。
![]()
![]()
其中 ![]()
![]() 表示从
表示从 ![]() 到
到 ![]() 长度为
长度为 ![]() 的通路数
的通路数 ![]() 或回路数
或回路数 ![]() 。
。
![]() 为
为 ![]() 中长度为
中长度为 ![]() 的通路总数,其中
的通路总数,其中 ![]() 为
为 ![]() 中长度为
中长度为 ![]() 的回路总数。
的回路总数。
(2) 设 ![]()
则 ![]() 中元素
中元素 ![]() 为
为 ![]() 中
中 ![]() 到
到 ![]() 长度小于等于
长度小于等于 ![]() 的通路总数,
的通路总数, ![]() 为
为 ![]() 中长度小于等于
中长度小于等于 ![]() 的通路总数,其中
的通路总数,其中 ![]() 为
为 ![]() 中长度小于等于
中长度小于等于 ![]() 的回路总数。
的回路总数。
例4、在例3的有向图
![]() 中,
中,
(1) 求 ![]() ,
, ![]() ,
, ![]() 。
。
(2) 求 ![]() 到
到 ![]() 长为
长为 ![]() 的通路数,
的通路数, ![]() 到
到 ![]() 长为4的通路数,
长为4的通路数,
![]() 到自身长为
到自身长为 ![]() 的回路数,
的回路数, ![]() 中长为
中长为 ![]() 的通路总数。
的通路总数。
解:(1)  ,
, 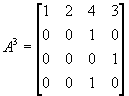 ,
,
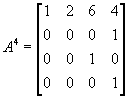
(2) ![]() 到
到 ![]() 长为
长为 ![]() 的通路数是
的通路数是 ![]() ,
,
![]() 到
到 ![]() 长为
长为 ![]() 的通路数是
的通路数是 ![]() ,
,
![]() 到自身长为
到自身长为 ![]() 的回路数是
的回路数是 ![]() ,
,
![]() 中长为
中长为 ![]() 的通路总数是
的通路总数是 ![]() (
( ![]() 中所有元素之和)。
中所有元素之和)。
设 ![]() 为有向图,
为有向图, ![]() ,令
,令
![]() ,
, ![]()

可达性矩阵 ![]()
其中元素 ![]() 可由
可由 ![]() 求得,
求得,