平面图
重点：1、平面图的概念，
2、常见的非平面图 
， 
，
3、平面图中面的次数与边数关系 
，
4、平面图的欧拉公式 
。
1、定义：一个图 
如果能以这样的方式画在平面上：除顶点处外没有边交叉出现，则称
为平面图，画出的没有边交叉出现的图称为
的一个平面嵌入或
的一个平面图。
例1、 
以上图中，(1)即 
图，(2)是(1)的平面嵌入，故(1)是平面图。
(4)是(3)的平面嵌入，故(3)是平面图。
(5)即
图，无论怎样画，都不可能将交叉的边全去掉，(6)是(5)的一种画法。同样，(7)即
图，无论怎样画，也不可能将交叉的边全去掉，(8)是(7)的一种画法。故
和
都不是平面图。
2、极大平面图，极小非平面图。
极大平面图——若在平面图
中任意不相邻的两个顶点之间再加一条边，所得图为非平面图，则
为极大平面图。
极小非平面图——若在非平面图
中任意删除一条边后，所得图是平面图，则
为极小非平面图。
例如： 
，
为极大平面图，
和
都是极小非平面图。
1、定义：设
是一个连通的平面图 (指
的某个平面嵌入)，
面——平面图的区域 (回路围成的)，
无限面 (外部面)——面积无限的区域，记 
，
有限面 (内部面)——面积有限的区域，
边界——包围面的边 (回路)，
次数——面 
边界的长度，记 
。
若
是非连通的平面图，设
有 
个连通分支，则
的无限面
的边界由 
个回路形成。
例2、
如上图所示的连通平面图，共有 
个面 
，其中 
的边界 
， 
， 
的边界 
， 
，
的边界为复杂回路 
， 
。
注意：(1) 一个平面图的无限面只有一个。
(2) 同一个平面图可以有不同形状的平面嵌入 (互相同构)。
(3) 不同的平面嵌入可能将某个有限面变成无限面，而将无限面变成有限面。
例3、
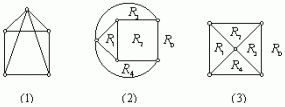
图(2)，(3)都是图(1)的平面嵌入，图(2)中， 
，图(3)中， 
，它们虽然形状不同，但都与(1)同构。
2、平面图中面次数与边数的关系。
( 
为面数)
3、欧拉公式。
设
为连通的平面图，顶点数为 
，边数为 
，面数为
，则
如例3中，图(1) 
， 
，则 
。