二部图（偶图）

重点：二部图的定义及判定。

一、二部图（偶图）的定义

1、若存在无向图的顶点集的一个划分，，，使得中任何一条边的两个端点分别在和中，则称为二部图 (或偶图)。

　　其中称互补顶点子集，记为。

2、完全二部图 (或完全偶图)。

　　若中任一顶点与中每一顶点均有且只有一条边相关联，则称此二部图为完全二部图 (或完全偶图)。

　　若，，则记完全二部图为。

　　例1、
　　

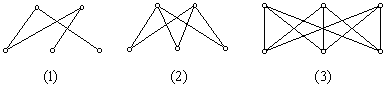
　　上图中，(1)，(2)，(3)都是二部图，其中(2)，(3)分别是完全二部图和。

二、判定定理

　　一个无向图是二部图当且仅当中无奇数长度的回路。

　　例2、判断以下是否二部图。

　　解：(1)，(2)，(3)是二部图，其中(2)，(3)分别与例1中的(2)，(3)同构，即和。

　　图(1)中所有的回路长度均为偶数。(思考，求其互补顶点子集)

　　图(4)不是二部图，因图中存在长为的回路。