树与生成树
重点：1、无向树的定义 (包括等价定义)，
2、无向树的性质，
3、生成树的定义，由连通图构造最小生成树的方法。
1、无向树——连通且不含回路的无向图。
无向树简称树，常用 
表示。
平凡树——平凡图。
森林——连通分支数大于等于 
，且每个连通分支都是树的无向图。
例1、
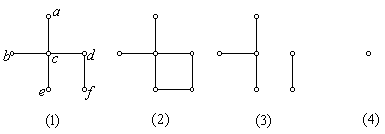
上图中，(1)与(4)是树，(4)为平凡树。(2)有回路，不是树。(3)不连通，也不是树，但它有 个连通分支，每个连通分支都是树，故(3)是森林。
(1)所示的树中， 
是树叶， 
是分支点。
2、树的六个等价定义。
定理：设 
， 
， 
，
(1) 
连通且不含回路，
(2) 的每对顶点间具有唯一的路径，
(3) 连通且 
，
(4) 无回路且 ，
(5) 无回路，但在 中任两个不相邻的顶点之间增加一条边，就形成唯一的一条初级回路，
(6) 是连通的，但删除任何一条边后，就不连通了。
3、性质。
设 
为无向树， ， ，由树的等价定义(3)即得
(1)
树中顶点数与边数的关系： ，
(2)定理：非平凡树至少
片树叶。
证明：设
为 
阶非平凡树，设 有 
片树叶，
则有 
个顶点度数大于等于
，由握手定理，
又由(1) 
，代入上式，解得 
，即
至少
片叶。
例2、画出所有的 
个顶点的非同构的树。
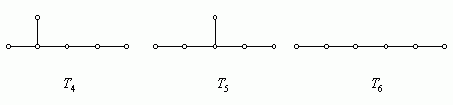
解：所要画的树有
个顶点，则边数为 
，因此 个顶点的度数之和为 
，可以产生以下五种度数序列：
(1) 
(2) 
(3) 
(4) 
(5) 
其中序列(1)，(2)，(3)，(5)各画一棵，分别对应以下的树 
，而(4)中有
棵非同构的树，对应以下的 
。
例3、(1) 一棵树有 
片叶， 
个
度顶点，其余都是 
度顶点，求 度顶点多少个？
(2)
一棵树有
个
度顶点，
个
度顶点，其余都是树叶，求这棵树共有多少个顶点？
解：(1) 设有
个 度顶点，则顶点数 
，边数 
，
由握手定理，
，
解得 
，
故这棵树有
个 度顶点。
(2)
设有
片树叶，则顶点数 
，边数 
，
由握手定理，
解得 
，
故顶点总数为
个。
1、定义：设
是无向连通图， 是 的生成子图，若
是树，称
是
的生成树。
树枝——
在
中的边，
弦——
不在
中的边，
余树——
的所有的弦的集合的导出子图。
例4、
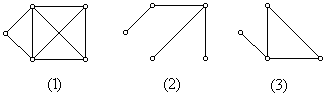
上图中，(2)是(1)的生成树，(3)是(2)的余树。
注意：(1) 生成树不唯一 (思考：求出上图中与(2)不同的生成树)
(2) 余树不一定是树。
2、连通图的性质。
设 为连通图， ， ，
(1) 至少有一棵生成树，
(2) 
，
(3)
设
是
的生成树， 
是 的余树，则 中有 
条边。
已知连通图 ，求其生成树步骤：
若 无回路，则 本身就是树，若
中有回路 
，则删除
上任一边，不影响图的连通性，若还有回路，就再删除此回路上的一条边，直到图中无回路为止，得到的即 的生成树。
3、最小生成树。
对于有向图或无向图 的每条边附加一个实数 
，则称
为边 
上的权， 连同附加在各边上的实数称为带权图，记为 
。
定义：设无向连通带权图
，
是
的一棵生成树， 各边带权之和称为
的权，记作 
， 的所有生成树中带权最小的生成树称为最小生成树。
求最小生成树的方法—— 
避圈法。
设 阶无向连通带权图
中有 
条边 
，它们带的权分别为 
，不妨设 
，
(1)
取 
在
中 (非环，若
为环，则弃 )，
(2)
若 
不与
构成回路，取 在 中，否则弃 ，再查 
，继续这一过程，直到形成树为止。
例5、求以下连通图的最小生成树
及
。
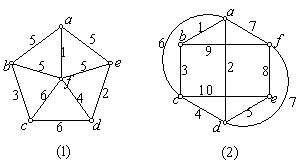
解：所求最小生成树如下：
， 
，
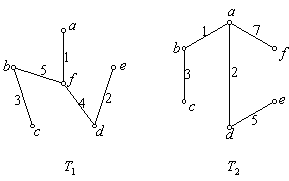
注意： 的最小生成树可能不唯一，但
的不同最小生成树权的值一样。