集合的基本运算
重点：(1)
掌握集合的运算 
，
(2) 用文氏图表示集合间的相互关系和运算，
(3) 掌握基本运算律的内容及运用。
集合 
的并集 
，交集 
，相对补集 
，绝对补集 
，对称差 
。
，
(当 
时，称 不交)
以上定义加以推广，可得
个集合的并集，交集：
，
，
，
(其中 
为全集)，
。
例1、设 
， 
， 
， 
，求出以下集合。
(1)
，
(2) 
，
(3)
，
(4) 
，
(5)
，
(6) 
，
(7) 
，
(8) 
。
解：(1) 
，
(2) 
，
(3) 
，
(4) 
，
(5) 
，
(6) 
，
(7) 
，
(8) 
。
1、文氏图。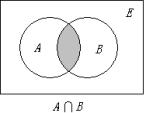 
(1)
用大矩形表示全集
，
(2) 矩形内的圆表示集合，
(3) 除特殊情形外，一般，表示两个集合的圆是相交的，
(4) 圆中的阴影的区域表示新组成的集合。
2、用文氏图表示集合的有关运算。
例2、用文氏图表示下列集合。
(1) ，
(2) 
，
(3) 
，
(4) 
。
解：
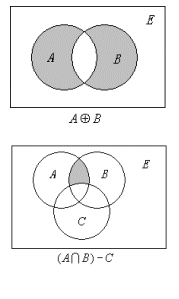
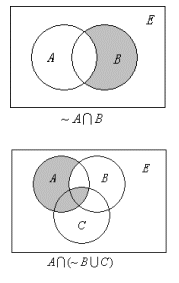
例3、用集合公式表示下列文氏图中的阴影部分。
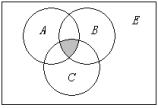
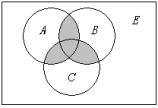
(1) (2)
解：(1) 
(2) 
1、幂等律： 
， 
2、结合律： 
， 
3、交换律： 
， 
4、分配律： 
，
5、同一律： 
， 
6、零律： 
， 
7、互否律： 
(排中律)， 
(矛盾律)
8、吸收律： 
， 
9、德·摩根律： 
10、双重否定律： 
以上恒等式的证明思路：欲证 
，即证对任意 
， 
。
例4、证明分配律
。
证明：对任意
，
故 。
除基本运算外，还有以下一些常用性质 (证明略)
11、 
， 
12、 
， 
13、 
14、 
15、 
16、 
“ 
”的交换律
17、 
“ ”的结合律
18、 
19、 
20、 
例5、证明：
(第14条)
证明：对任意
，
故 。
例6、证明 
。
证明：
10条基本定律及10条性质可用于证明 (如例6)，化简。
例7、化简 
解：因为 
，
所以 
，
又因为 
，
所以 
，
所以原式化简为
，
又 
，
最后，原式化简为
。
例8、设 
均为
的子集，以下命题中为真，为假的各有哪些？
(1) 
，
(2) 
，
(3) 
，
(4) 
，
(5) 
，
(6) 
。
解：为真的命题有(1)、(3)、(5)，为假的命题有(2)、(4)、(6)。