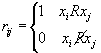集合的笛卡儿积和二元关系
重点：(1) 掌握有序对的概念，
(2) 笛卡儿积及性质，
(3) 二元关系的定义及三种表示法，
(4) 一些特殊的二元关系。
1、有序对，记 
，其中 
为第一元素， 
为第二元素 (注意顺序)
特点：(1) 
时， 
，
(2) 
。
有序 
元组 
，记 
。
2、笛卡儿积。
定义：集合 
和 
的笛卡儿积，记作 
。
。
例1、 
，求 ， 
， 
， 
， 
。
解：
， 
。
例2、设 
，求 
。
解：
，
。
注意：(1) 若
是 
元集， 是 元集，则 为 
元集。
(2) 笛卡儿积是集合，有关集合的运算都适合。
(3) 一般，
(只有当 
，或 
中有一个是空集时，才有 
)。
3、笛卡儿积运算对 
或 
满足分配律。
(1) 
(2) 
(3) 
(4) 
例3、证明：
。
证明：对任意 ，
故 。
4、
阶 
笛卡儿积。
特别，当 
时，记为 
。
如
， 
。
1、定义：(1) 若集合
为空集或它的元素都是有序对，则称
为二元关系。若 
，则记作 
，否则，记作 
。
(2)
的任何子集都称作从
到
的关系，特别，当 
时，称作 
上关系。
例4、 ， 
设 
，
，
，
。
则 
都是从
到
的关系。
2、
上不同关系的数目。
若
为
元集，记 
，则 
，
的子集共有 
个，每个子集都是
上的一个关系，所以，
元集
上不同的关系共有
个。如 
元集
上共有 
个不同关系。
3、特殊的关系。
空关系 
，全域关系 
，恒等关系 
。
对任意集合
，
空关系
，
全域关系 
，
恒等关系 
。
4、常用关系。
(1)
设 
，
上小于等于关系：
。
(2)
设 
，
上整除关系：
。
(3)
幂集 
上的包含关系
：
。
例5、 
，求 
， 
。
解：
，
。
例6、 ，求 上的包含关系 。
解：
，
5、
上二元关系的表示法。
二元关系有三种表示法，即集合表示法，矩阵表示法和关系图表示法。
例7、已知 
，
上关系 
，
求
的关系矩阵 
和关系图。
解：
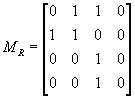，关系图：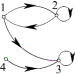 
注意：关系的三种表示法中，可由其中一种求出另外两种。
一般：设 
，其中 
